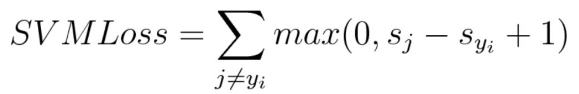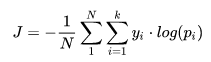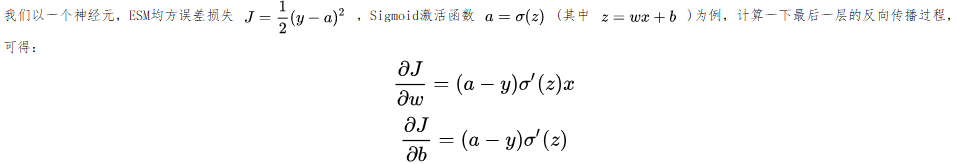【机器学习】常见的损失函数 |
您所在的位置:网站首页 › 损失函数 代价函数 目标函数 › 【机器学习】常见的损失函数 |
【机器学习】常见的损失函数
|
目录 1. 损失函数、代价函数与目标函数 2. 回归损失函数 2.1 均方误差/平方损失/L2 损失 2.2 平均偏差误差(mean bias error)/绝对值损失/L1损失 3. 分类损失 3.1 0-1损失 3.2 对数损失(对数似然损失) 3.3 Hinge Loss/SVM 损失 3.4 交叉熵损失/负对数似然: 4. 二次代价函数与交叉熵函数的对比 4.1 二次代价函数+sigmoid函数 4.2 交叉熵损失函数+sigmoid函数 5.分别从极大似然和熵的角度来看交叉熵损失 1. 损失函数、代价函数与目标函数 损失函数(Loss Function):是定义在单个样本上的,是指一个样本的误差。代价函数(Cost Function):是定义在整个训练集上的,是所有样本误差的平均,也就是所有损失函数值的平均。目标函数(Object Function):是指最终需要优化的函数,一般来说是经验风险+结构风险,也就是(代价函数+正则化项)。从学习任务的类型出发,可以从广义上将损失函数分为两大类——回归损失和分类损失,这里都是单样本的损失 2. 回归损失函数 2.1 均方误差/平方损失/L2 损失其公式为
python实现:
python实现:
也就是说,当预测错误时,损失函数为1,当预测正确时,损失函数值为0。该损失函数不考虑预测值和真实值的误差程度。只要错误,就是1。 优势:直观的刻画分类的错误率缺点:因为其非凸,非光滑的特点,使得算法很难对其进行直接优化 3.2 对数损失(对数似然损失)
事实上,该损失函数用到了极大似然估计的思想。P(Y|X)通俗的解释就是:在当前模型的基础上,对于样本X,其预测值为Y,也就是预测正确的概率。由于概率之间的同时满足需要使用乘法,为了将其转化为加法,我们将其取对数。最后由于是损失函数,所以预测正确的概率越高,其损失值应该是越小,因此再加个负号取个反。 可以说对数损失就是采用极大似然估计并且取对数得到的损失函数。推导如下: 假设样本为X,其对应的类别为Y,P(Y|X)就是在当前模型的基础上,给定X正确判断为Y的后验概率。我们希望每一个样本X被正确预测到相应类别Y的概率都最大,即max P(Y|X),那么所有样本正确预测概率相乘最大化就是我们所期望的,因此采用极大似然的原理。 Step1:构建似然函数
我们的目标是希望对数似然函数更大,即
对于单个样本有 简言之,在一定的安全间隔内(通常是 1),正确类别的分数应高于所有错误类别的分数之和。因此 hinge loss 常用于最大间隔分类(maximum-margin classification),最常用的是支持向量机。尽管不可微,但它是一个凸函数,因此可以轻而易举地使用机器学习领域中常用的凸优化器。 数学公式:
思考下例,我们有三个训练样本,要预测三个类别(狗、猫和马)。以下是我们通过算法预测出来的000每一类的值:
计算这 3 个训练样本的 hinge loss: ## 1st training example max(0, (1.49) - (-0.39) + 1) + max(0, (4.21) - (-0.39) + 1) max(0, 2.88) + max(0, 5.6) 2.88 + 5.6 8.48 (High loss as very wrong prediction) ## 2nd training example max(0, (-4.61) - (3.28)+ 1) + max(0, (1.46) - (3.28)+ 1) max(0, -6.89) + max(0, -0.82) 0 + 0 0 (Zero loss as correct prediction) ## 3rd training example max(0, (1.03) - (-2.27)+ 1) + max(0, (-2.37) - (-2.27)+ 1) max(0, 4.3) + max(0, 0.9) 4.3 + 0.9 5.2 (High loss as very wrong prediction) 3.4 交叉熵损失/负对数似然:交叉熵损失函数有两种表达形式,第一种形式是:
其中,yi是类别i的真实标签;pi是类别i的概率值;k是类别数,N是样本总数。这种交叉熵函数一般用在softmax层的后面。 第二种形式是:
这种形式就不对应softmax层了,而是sigmoid。sigmoid作为最后一层输出的话,那就不能把最后一层的输出看作成一个分布了,因为加起来不为1。现在应该将最后一层的每个神经元看作一个分布,对应的 target 属于二项分布(target的值代表是这个类的概率),那么第i 个神经元交叉熵为:
那么总的交叉熵函数就为:
可以看到最后一层反向传播时,所求的梯度中都要乘以sigmoid的导数,而sigmoid的导数的图像如下,当神经元输出接近1时候,Sigmoid的导数就会很小,这样
想要解决这个问题,需要引入接下来介绍的交叉熵损失函数。这里先给出结论:交叉熵损失+Sigmoid激活函数可以解决输出层神经元学习率缓慢的问题,但是不能解决隐藏层神经元学习率缓慢的问题。 4.2 交叉熵损失函数+sigmoid函数
可以看到sigmoid的导数被约掉,这样最后一层的梯度中就没有 见博客【机器学习】分别从极大似然和熵的角度来看交叉熵损失
|
【本文地址】


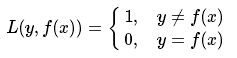
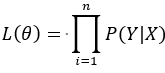
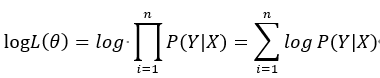
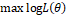 ,等价于使负的对数似然函数最小,即
,等价于使负的对数似然函数最小,即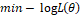 。因此损失函数为:
。因此损失函数为: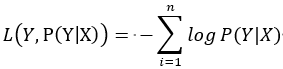
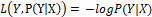 ,对数(似然)损失函数由此而来。
,对数(似然)损失函数由此而来。